Cryptography & Challenges posed by Quantum Computers

Abstract

Most of the security protocols today employ a combination of symmetric key encryption and asymmetric key encryption. Asymmetric key algorithms are computationally expensive but provide ease of use since their public keys can be easily distributed. Symmetric key algorithms are many times faster than asymmetric key algorithms. However, it is a challenge to distribute symmetric keys among participants. Security protocol designers usually combine both types of algorithms and use symmetric algorithms for data encryption and asymmetric key algorithms for establishing shared secrets (symmetric key). The public key of the asymmetric keys pair is currently shared using public key infrastructure (PKI).
Quantum computers can break most of the asymmetric key algorithms but cannot break symmetric key algorithms with larger key size. Researchers are working on quantum secure methods for exchanging/establishing symmetric keys so that these can replace the existing PKI infrastructure that has become vulnerable to attack using quantum computers. One group of these methods utilize quantum physics principles for establishing key and are called the Quantum Key Distribution method (QKD). These require a new physical channel and quantum physics-based secure mechanism to distribute the large symmetric keys among communicating parties. Another group of methods depends on mathematical problems that are difficult even for quantum computers, these methods are called Post Quantum Cryptography (PQC).

What is Cryptography?

Cryptography is the art and science of protecting information by writing it secretly, which prevents third parties or the public from reading sensitive information. The process of scrambling the information to make it unreadable is called Encryption, and this scrambled information is called cipher text. The decryption process converts scrambled information to the original form or plain text. Cryptography helps maintain the confidentiality and integrity of important information and has various usages spanning multiple domains.

Symmetric key cryptography:

“Symmetric key” cryptography and “public key” cryptography are two categories of cryptography. Here “key” refers to the information known to parties involved and is used to encrypt/decrypt information.
Symmetric key cryptography uses the same key to encrypt information and decrypt information. One of the challenges of symmetric key cryptography is securely communicating the key to all the concerned parties without divulging it to adversaries. Some popular symmetric key cryptography algorithms are AES, DES, and IDEA.

Asymmetric key cryptography:

Instead of using one key, asymmetric key cryptography or public-key cryptography (PKC) uses a key pair. One of the keys of this key pair is called the public key. The public key can be known to everyone and is used to encrypt the information. Another key of the key pair is called the private key. The private key is kept secret and used for decryption. Asymmetric key cryptography allows anyone holding the public key to encrypt the information. However, only the person with the secret private key can decrypt it. Digital signatures schemes (DSA), end-to-end E-Mail encryptions (OpenPGP), secure transport layer protocol (SSL), and many other security protocols use Asymmetric key cryptography. Some asymmetric key cryptography algorithms are RSA, Diffie-Hellman, and ECC.
Public and Private Keys used in PKC algorithms are mathematically related, which means that the security of PKC hinges on the difficulty of solving complex mathematical problems to derive one key from another. All PKC algorithms depend on the complexity of solving complicated mathematical problems using conventional computers. Some of these complex problems used in cryptography are prime factorization of large numbers or solving discrete logarithm problems. One of the most popular and widely used cryptographic algorithms, RSA, is based on prime factorization. Diffie-Hellman and ECC algorithms depend on solving discrete logarithm problems.
PKC algorithms with a decent key size are considered secure for conventional computers. It is not possible or is very time/resource-consuming for classical computers to be able to solve the mathematical problems that form the basis of these PKC algorithms. All this will change with the advent of quantum computing.

Quantum Computers

Noted physicist Feynman conceptualized the idea of using the effects of quantum mechanics in a computer. In contrast to bits of the conventional computer that can take 0 or 1 values, fundamental blocks of quantum computer qubits can exist in 0, 1, or simultaneously in both states. Phenomena of qubits entanglement result in a tremendous increase in the possibility of parallel processing. An n-qubit quantum computer can process 2n operations in parallel. Several companies have been working on building quantum computers. IBM Quantum System One is a 27-qubit computer, and Intel has 49 qubit processors; however, Quantum computers are so far not available for wide usage.
Quantum computers threaten cryptographic algorithms because they can perform many times more parallel operations than conventional computers. Quantum computers can break PKC by solving complex mathematical problems or break symmetric key cryptography by exhaustively searching for all possible secret keys.

How Quantum Computers are a Threat to Cryptography?

Mathematician Peter Shor published a Quantum computers algorithm for large integer prime factorization and discrete logarithm problems. Shor’s algorithm makes it possible to break widely used RSA, Diffie-Hellman, and ECC algorithms using quantum computers. Shor’s algorithm would require a 1000-qubit computer to break 160-bit ECC and a 2000-qubit computer to break 1024-bit RSA. Quantum computers with this kind of processing power do not exist today. However, they may become available in the future. There are reports that hackers have been collecting encrypted data with the hope that, in the future, they will be able to decrypt it using quantum computers and make monetary and political gains out of it.

Indian-origin Computer scientist Lov Grover developed a Quantum computer algorithm for searching unsorted databases. Grover’s algorithm requires √N operations to search N entries, while conventional computers require N/2 operations to search N entries. For keys of smaller size, Grover’s algorithm can break the symmetric key algorithm DES.
Grover’s algorithm can exhaustively search for keys of symmetric-key algorithms. However, the number of operations needed to perform search increases exponentially with an increase in key size. The security offered by Symmetric key Algorithms like DES and AES improves with an increase in key size. AES algorithm with a key of 256 bits is considered safe from quantum computers.

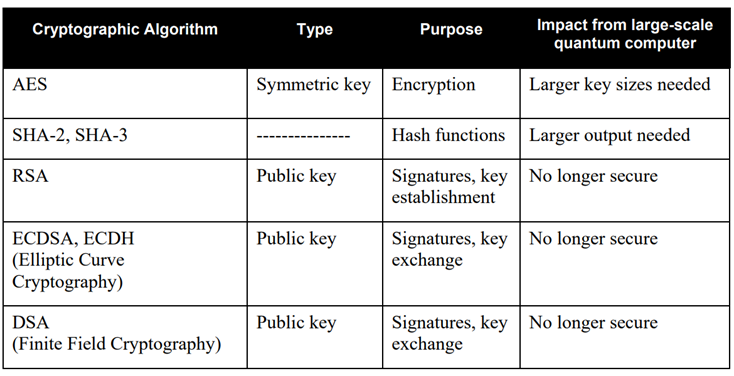
(Source: NISTIR 8105 Report on Post-Quantum Cryptography)

The Way Forward:

From the above discussion, it is clear that symmetric key cryptography will be secure even when quantum computers with thousands of qubits become available. However, new protocols shall be required to securely distribute shared keys since the current PKC-based shared key establishment mechanism will not withstand quantum computers.
Currently, two types of techniques are in development for secure key distribution. The first type of technique depends on computational problems that are difficult even for quantum computers and are called post-quantum cryptography. The second type of technique depends on the laws of quantum physics and is called Quantum key distribution.

Quantum Key Distribution

Quantum key distribution (QKD) methods allow the secure exchange of shared keys between two participants over an insecure channel. Laws of physics (characteristics of quantum mechanics) guarantee the security of key distribution, so an increase in computing power cannot break this security.
In QKD, the information that needs to be exchanged is encoded as quantum states of light. Following Quantum physics concepts form the basis of the security of QKD:
1. Heisenberg’s uncertainty principle implies that the act of measuring an unknown quantum state modifies the state. So, if an eavesdropper measures the data(qubit) during transmission, the value of the data(qubit) will change.
2. It is physically impossible to make a perfect copy of an unknown quantum state, so an eavesdropper can’t copy a bit stream and measure it later.
3. Properties of quantum entanglement limit the information that third parties may obtain.

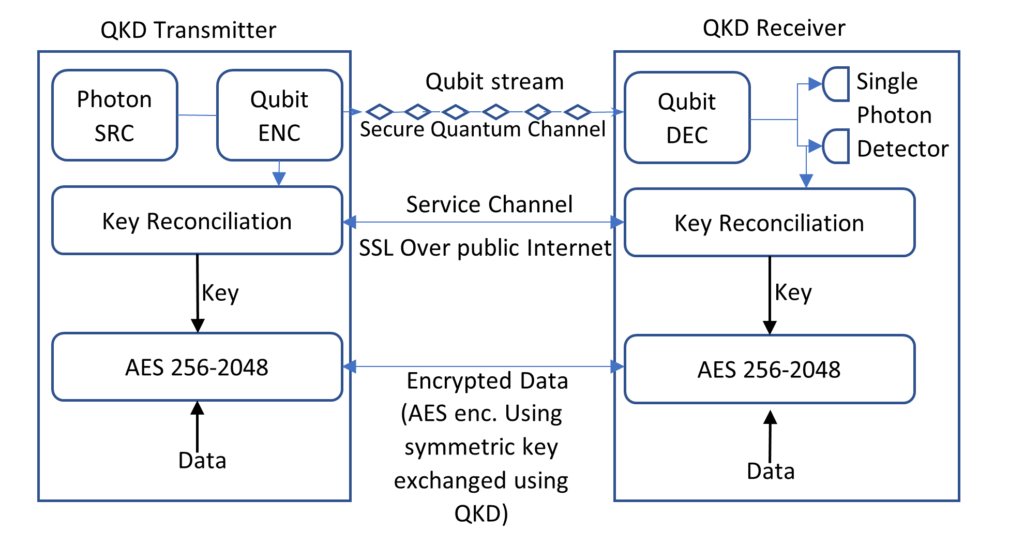
Quantum key distribution uses two communication channels, one channel can be an insecure authenticated public channel, and the second channel needs to be a quantum communication channel. The sender uses a light source to send a stream of photons through the quantum channel. Each one of these photons represents a bit of information. Before sending each photon, the sender randomly chooses the measurement basis for the photon and records both the measurement basis and the value of the bit. The receiver also randomly chooses one of the two measurement basis and records both the selected basic and measured values. After transferring all the bits, the sender and receiver exchange the measurement basis used to measure each bit. Since both sender and receiver randomly selected measurement basis, it will be the same for some of the bits. The value of the bits for which the sender and receiver used the same measurement basis forms the shared secret key. Since only measurement basis is exchanged on the unsecured channel and not the actual measurement, the sender and receiver can construct the key; however, the eavesdropper can’t.

Post Quantum Cryptography

Post Quantum Cryptography (PQC) algorithms consist of mathematical problems that are considered difficult for conventional computers, as well as for quantum computers. Some of the methods that fall under PQC methods are code-based cryptography, Multivariate based cryptography, and Lattice-based cryptography. In 2016 NIST launched the Post Quantum Cryptography project, which aims to standardize a few Quantum resistant cryptography systems. In 2016 NIST floated a request for submission for PQC algorithms. The evaluation process for PQC started with 69 algorithms. After round 3 of evaluation in July 2020, NIST has narrowed it down to four key exchange algorithms and three digital signature algorithms. On July 5, 2022, NIST declared that they have selected the CRYSTALS-Kyber KEM algorithm and 3 digital signature algorithms for standardization. These OQS implementations can help in prototyping Quantum resistant cryptography.

HSC is currently working on projects where PQC algorithms are being used to safeguard VPN and E-Mail products. Our team has also worked on the implementation of the QKD post-processing algorithm. If you are interested in this technology and its applications then let us connect!